Magisk summa hos en normal magisk kvadrat
Dela
Magisk summa hos en normal magisk kvadrat av ordningen n
I mitt tidigare blogginlägg beskrev jag en normal magisk kvadrat av ordning 3, alltså en 3x3-matris med siffror. Den magiska summan hos denna magiska kvadrat är 15.
Men vilken är den magiska summan hos en normal magisk kvadrat i det allmänna fallet?
Tja, vi kan använda samma beräkningsprincip som för den 3x3 magiska kvadraten!
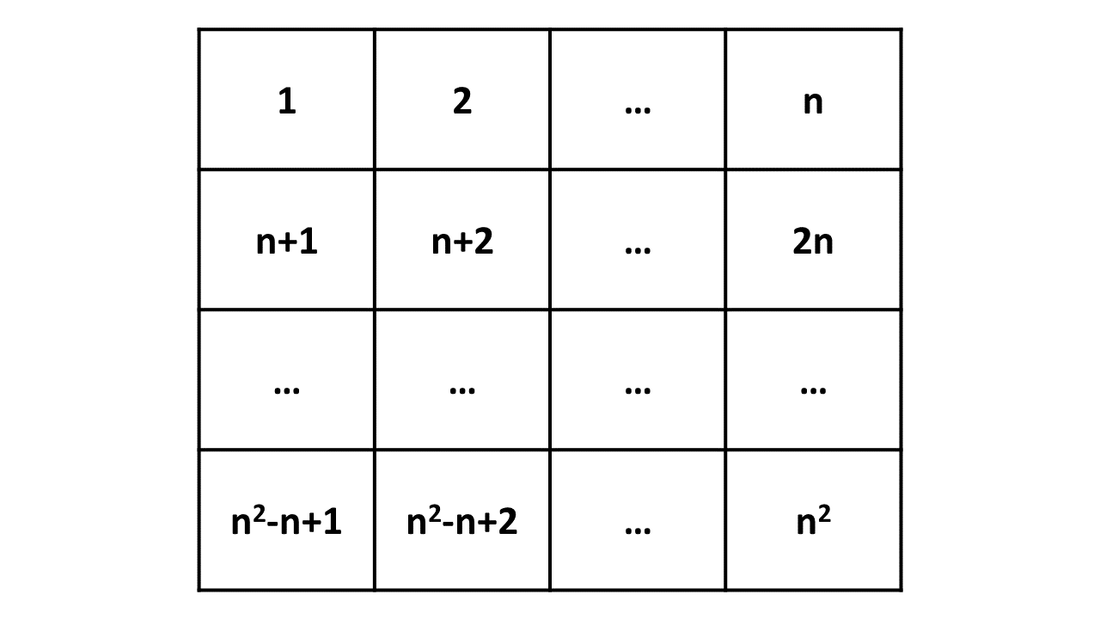
För en normal magisk kvadrat börjar talserien med en '1' och består av naturliga tal i en stigande sekvens.
Den magiska kvadraten av ordning n, består av n rader och n kolumner, dvs det finns n2 tal.
Först beräknar vi summan 'S' av alla tal i den magiska kvadraten. För att göra detta kan vi använda ett litet knep som du kanske kommer ihåg från skolan.
I den första raden i tabellen nedan skriver vi alla tal i stigande ordning. Summan av denna rad är S.
I den andra raden i tabellen skriver vi talen i fallande ordning. Summan av denna rad är naturligtvis också S, eftersom det är samma tal men i en annan ordning.
| S= | 1 | 2 | 3 | ... | n2 |
| S= | n2 | n2-1 | n2-2 | ... | 1 |
| 2*S= | n2+1 | n2+1 | n2+1 | ... | n2+1 |
Om vi kolumnvis adderar cellerna i de två raderna finner vi att summan i varje kolumn är lika. Summan av den sista raden i tabellen blir då n2*(n2+1), eftersom antalet celler är n2 och innehållet i varje cell är n2+1. Denna summa är lika med 2*S.
Summan av alla tal i den magiska kvadraten blir då: S = n2*(n2+1)/2.
Den magiska kvadraten består av n rader. För att få summan av varje enskild rad måste vi alltså dela med n, dvs den magiska summan blir då lika med n*(n2+1)/2 !
Låt oss kontrollera detta resultat med resultatet i mitt tidigare blogginlägg genom att infoga n=3 i formeln ovan!
n*(n2+1)/2 = 3*(32+1)/2 = 15. Ja, den generiska formeln matchar det tidigare resultatet!
